Come trovare i lati di un triangolo rettangolo? Fondamenti di geometria

Le gambe e l'ipotenusa - lato di un triangolo rettangolo. Prima - questo è i segmenti che sono adiacenti ad angolo retto e l'ipotenusa è la parte più lunga della figura e si trova di fronte al angolo 90^su. Un triangolo pitagorico è quello i cui lati sono uguali ai numeri naturali; La loro lunghezza in questo caso è chiamata "tripla pitagorica".

Triangolo egiziano

Affinché l'attuale generazione riconoscala geometria nella forma in cui viene insegnata a scuola ora, si è evoluta per diversi secoli. Il punto fondamentale è il teorema di Pitagora. I lati di un triangolo rettangolare (la figura è conosciuta in tutto il mondo) sono 3, 4, 5.

Poche persone non hanno familiarità con la frase "I pantaloni pitagorici in tutte le direzioni sono uguali". Tuttavia, in realtà, il teorema suona come questo: c² (quadrato dell'ipotenusa) = a²+ b² (la somma dei quadrati delle gambe).

Tra i matematici, un triangolo con i lati 3, 4,5 (cm, m, ecc.) È chiamato "egiziano". È interessante notare che il raggio del cerchio, che è inscritto nella figura, è uguale a uno. Il nome sorse intorno al V secolo aC, quando i filosofi della Grecia viaggiarono in Egitto.

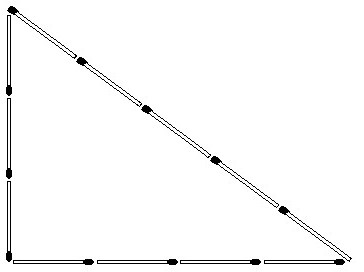
Quando costruivano le piramidi, architetti e geometri utilizzavano il rapporto 3: 4: 5. Tali strutture si sono rivelate proporzionate, piacevoli nell'aspetto e spaziose, e anche raramente collassate.

Per costruire un angolo retto, i costruttori usavano una corda, sulla quale erano legati 12 nodi. In questo caso, la probabilità di costruire un triangolo rettangolare è stata aumentata al 95%.

Segni di uguaglianza

• Un angolo acuto in un triangolo rettangolo eil lato grande, che è uguale agli stessi elementi nel secondo triangolo, è un segno indiscutibile di uguaglianza delle figure. Tenendo conto della somma degli angoli, è facile dimostrare che anche i secondi angoli acuti sono uguali. Quindi, i triangoli sono gli stessi nel secondo segno.
• Quando due figure si sovrappongono l'una sull'altra, giriamoin modo che, combinati, diventino un triangolo isoscele. Secondo le sue proprietà, i lati, o più precisamente l'ipotenusa, sono uguali, così come gli angoli alla base, il che significa che queste cifre sono le stesse.

Con il primo segno è molto semplice dimostrare che i triangoli sono veramente uguali, la cosa principale è che i due lati più piccoli (cioè le gambe) sono uguali.

I triangoli saranno gli stessi sul tratto II, la cui essenza risiede nell'uguaglianza della gamba e nell'angolo acuto.

Proprietà di un triangolo ad angolo retto

L'altezza che è stata abbassata dall'angolo retto, divide la figura in due parti uguali.

I lati di un triangolo rettangolo e le sue medianeè facile imparare dalla regola: la mediana, che è abbassata all'ipotenusa, è uguale alla sua metà. L'area della figura può essere trovata sia dalla formula di Heron sia dall'affermazione che è uguale alla metà del prodotto delle gambe.

In un triangolo rettangolo, le proprietà dell'angolo di 30^su, 45^su e 60^su.

• Con un angolo di 30^su, va ricordato che la gamba opposta sarà 1/2 del lato più grande.
• Se l'angolo 45^su, quindi il secondo angolo acuto è anche 45^su. Questo suggerisce che il triangolo è isoscele e le sue gambe sono le stesse.
• La proprietà di angolo di 60^su è che il terzo angolo ha una misura di grado di 30^su.

L'area è facilmente riconoscibile da una delle tre formule:

1. attraverso l'altezza e il lato a cui è abbassato;
2. dalla formula di Heron;
3. sui lati e l'angolo tra di loro.

I lati di un triangolo rettangolo, o megliocateches, convergono con due altezze. Per trovare il terzo, è necessario considerare il triangolo formato, e quindi, con il teorema di Pitagora, calcolare la lunghezza richiesta. Oltre a questa formula, c'è anche un rapporto tra l'area raddoppiata e la lunghezza dell'ipotenusa. L'espressione più comune tra gli studenti è la prima, poiché richiede meno calcoli.

Teoremi applicati a un triangolo rettangolo

La geometria di un triangolo rettangolo include l'uso di teoremi come:

1. Il teorema di Pitagora. La sua essenza sta nel fatto che il quadrato dell'ipotenusaè uguale alla somma dei quadrati delle gambe. Nella geometria euclidea, questo rapporto è la chiave. Puoi usare la formula se hai un triangolo, per esempio, SNH. SN - ipotenusa, e deve essere trovato. Quindi SN²= NH²+ HS².
2. Il teorema del coseno. Generalizza il teorema di Pitagora: g²= f²+ s²-2fs * cos l'angolo tra di loro. Ad esempio, viene fornito un triangolo DOB. DB noto catetere e ipotenusa DO, è necessario trovare OB. Quindi la formula assume la forma data: OB²= DB²+ DO²-2DB * DO * cos dell'angolo D. Ci sono tre conseguenze: l'angolo del triangolo sarà acuto, se la lunghezza al quadrato del terzo è sottratta dalla somma dei quadrati dei due lati, il risultato dovrebbe essere inferiore a zero. L'angolo è ottuso, se l'espressione è maggiore di zero. L'angolo è una linea retta per zero.
3. Il teorema del seno. Mostra la dipendenza delle partiangoli opposti. In altre parole, questo è il rapporto tra le lunghezze dei lati dei seni degli angoli opposti. Nel triangolo HFB, dove l'ipotenusa è HF, ci saranno: HF / angolo sin B = FB / angolo sin H = HB / angolo sin F.